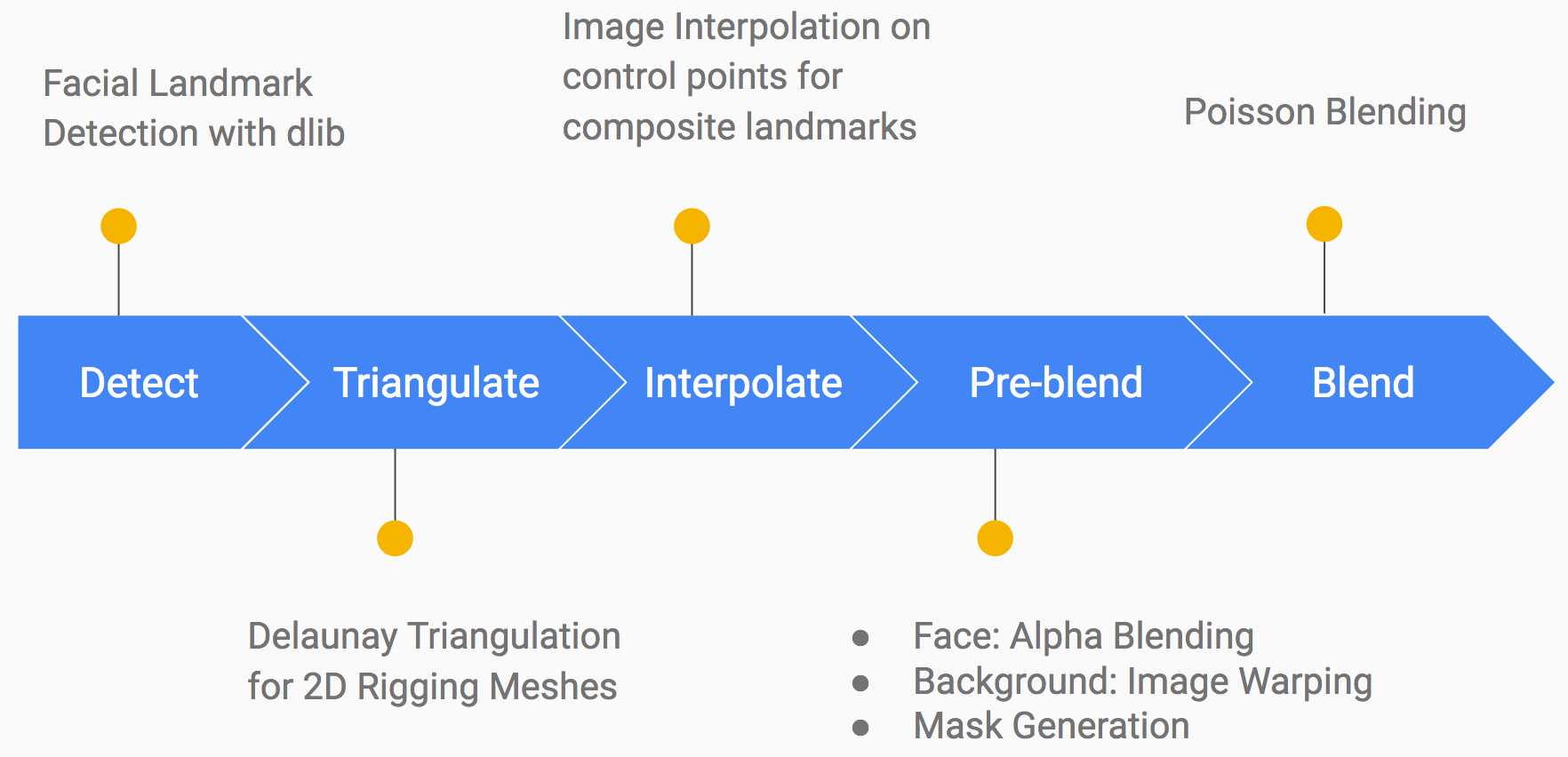
In this project we created a fully automatic program that produces photorealistic blends of distinct faces from profile pictures. We used various techniques including Delaunay triangulation, linear interpolation, affine transformation, and Poisson blending to create convincing results. We also leveraged external libraries such as OpenCV, Dlib, and Eigen in our process of manipulating the images.

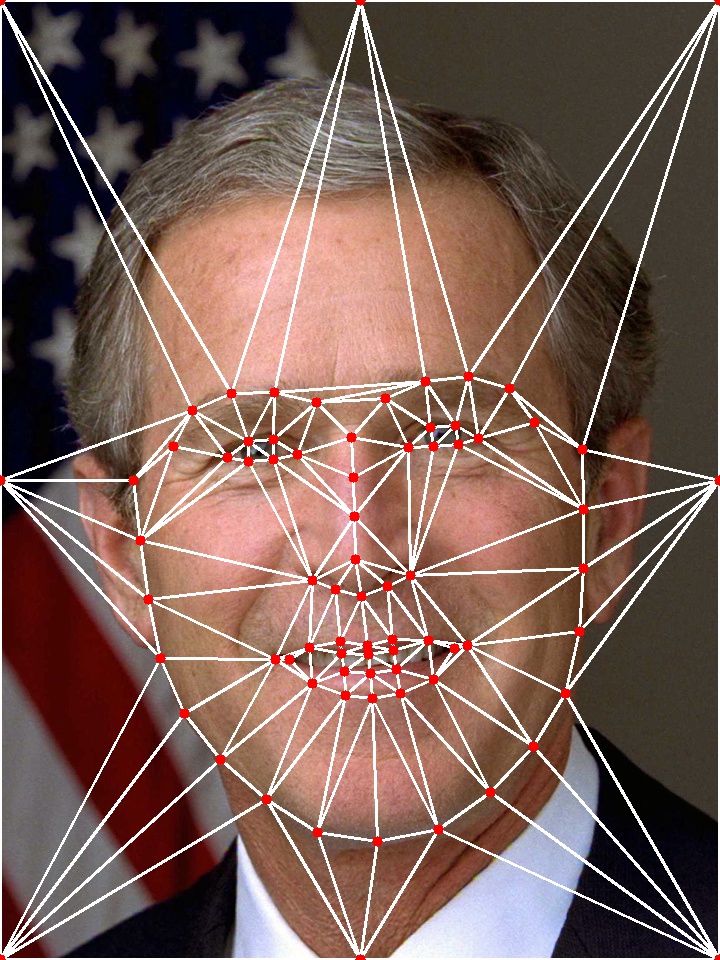
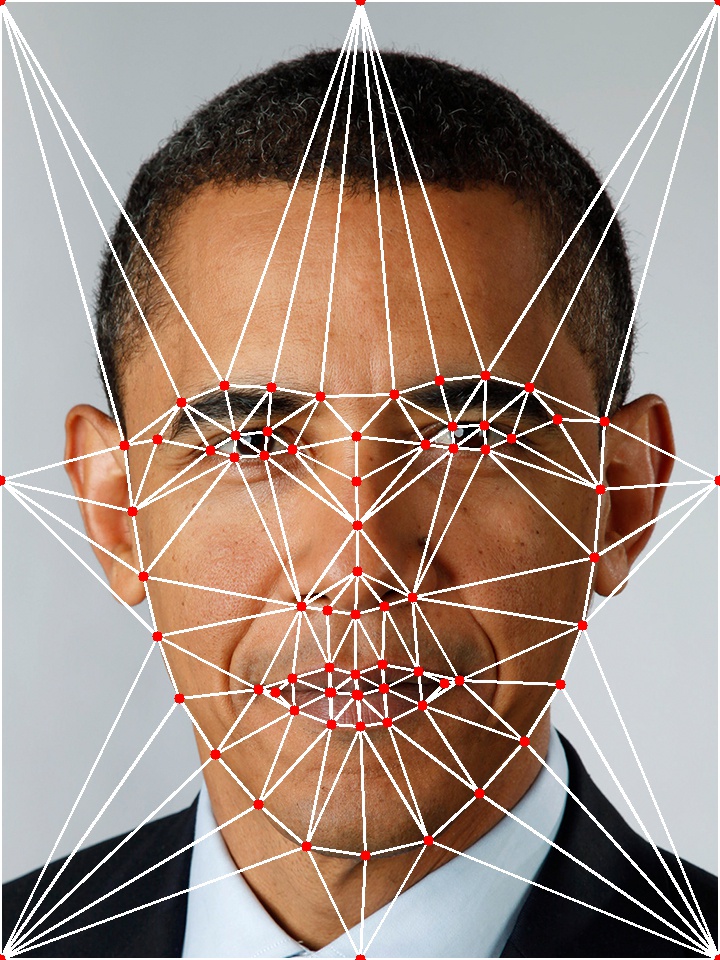
We used an external C++ toolkit, Dlib, to identify the face in the images and to extract 68 facial landmarks. Additionally, we also manually added 8 control points on the edges of the images in order to make the triangulation in the next stage cover the entire image.

|

|
We used Delaunay triangulation algorithm on control points of the destination image to create a 2D mesh. We chose to use Delaunay triangulation because it maximizes the minimum angle of all the angles in the triangulation, so that our mesh would have as few sliver triangles as possible. Both of us spent time understanding the algorithm and designed an implementation of incrementally inserting control points into the mesh. Upon each insertion we check if the Delaunay property (no point is inside the circumcircle of any triangle) is violated by any point in the resulting mesh, and if so we flip an edge connecting the point until the property is satisfied. However, in the interest of time, we ended up using OpenCV's implementation of Delaunay triangulation.
We then constructed a 2D mesh on the source image using the same topology as the mesh on the destination image so that the triangles on the two meshes form a one-to-one mapping relationship. Since Delaunay triangulation in no way guarantees to produce the same topology on human faces, we had to store the triangle mesh as triplets of indecies of the control points vector to create a mesh with the same topology on the other image.
|
|
We computed the resulting composite image's mesh as the linear interpolation of the two control meshes we created in step 2. By varing the interpolation parameter "alpha", we could control the likeliness of the composite face relative to the faces in the source image and the destination image.
In this step, we prepared the three ingredients for the final Poisson blending: an image with the composite face, a background image to blend the face into, and a blending mask that defines the edge where blending would happen.

|
First, we calculated the affine transformation from each triangle in the two control meshes to its corresponding triangle in the composite mesh. We then warped the source image and the destination image using the affine transformation, and blended them together by linearly interpolating the color of each pair of corresponding pixels. The interpolation parameter is the same alpha we used in step 3. This gives us the image of the composite face. The face is well-aligned since the large number of control points created a fine mesh that allowed us to align all the key landmarks. |

|
Second, we warped destination image so that its head would fit the composite face. |

|
Third, we build a face mask by feeding all the control points on the edge of the composite image's face into OpenCV's fillConvexPoly function. Note that we moved each control point's coordinates slightly (~2px) towards the center of the face so that the resulting face mask would be silightly smaller than the face on the warped destination image. This is to prevent any unwanted color bleeding in the final Poisson blending step. * Color bleeding is the phenomenon where the color on the blending edge diffuses into the blending area. This is a normal behavior of the Poisson blending algorithm. However, this can also leads to unwanted result if the blending edge is right on the edge between face and background, in which case the color of background (wall, cloth, etc.) can bleed into the blended face, creating a really disturbing look. |
Finally, we use Poisson blending algorithm to seamlessly stitch the linearly blended face onto the warped destination image. We chose Poisson blending because it hides the blending edge extreamly well.
Due to the lack of API support, both of us spend a lot of time reading the original paper that invented Poisson blending algorithm, and studied many blog posts as well as available lectures online to understand the algorithm well enough to implement it. Poisson blending blends images in the gradient domain rather than in the pixel domain. It enforces an edge constraint that the pixel value on the blending edge must be the same as the background image, and adjusts the pxiel values of the image being copied to minimize the change in the gradient domain compared to the original image. This allows Poisson blending to change pixel values gradually from the blending edge towards the center of the image, producing a seamless blend while maximumlly preserving the characteristics of the original image being copied. The solution to this optimization problem is a Poisson equation, hence the name "Poisson blending".
Solving the Poisson equation in the disceret case (e.g. images represented by discrete pixels) involves solving a linear system of equation Ax = b, where A is a huge sparse matrix and b is the target gradient vector mostly consisting of the original gradient values of the pixels in the blending area. We convolved a Laplacian kernel around the image being copied to get the values in vector b (modified entries on the edge to enforce the edge constraint). However, since the face being copied measures about 500px by 500px and therefore contains about 250,000 pixels, our matrix A would be 250,000 by 250,000 which certainly would not fit in RAM, so we had to store A as a sparse matrix. Even though OpenCV provides a sparse matrix struct, it provides no support for solving linear equations involving sparse matrix, so we ended up using a C++ template library for linear algebra called Eigen. We constructed matrix A and vector b in Eigen and used its Conjugate Gradient solver to solve the Poisson equation.


|

|
* Note on a few frames there is some color bleeding of Obama's black eyebrow into Trump's face.

|

|

|

|

|

|
We pair-programmed most of the code. Daiwei finished the rest because Provi has a Windows.
Daiwei came up with the original idea of doing face morph and found all the relevant online resources to guide implementation. Daiwei also came up with the idea of using Poisson image editing to solve the edge blending problem. Daiwei wrote the project proposal and this final report.
Provi was responsible for managing the Github repo, wrote the milestone report, and created final presentation slides. Provi came up with the idea of crop out the face and stitch it to one of the source image to avoid the blurry misalignment problem.
We spend a considerable amount of time exploring the possibility of doing real-time face swap/replacement on webcam. However, after we found that it is virtually impossible for us to make Poisson blending work under 100ms on 720P webcam, we abandoned the idea. Here are two screen shots of this half-way-killed work.

|

|